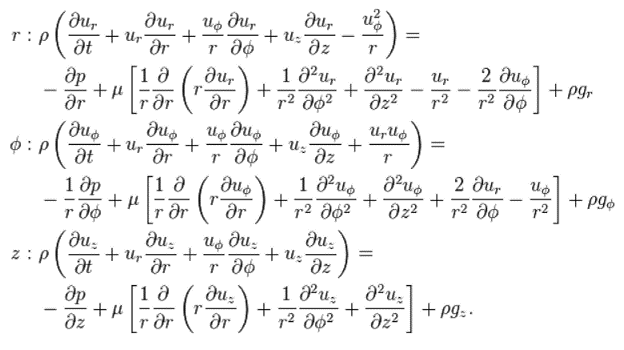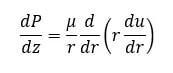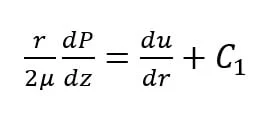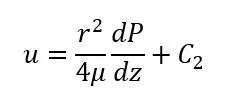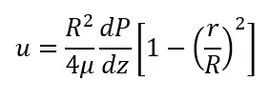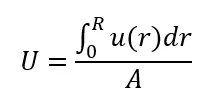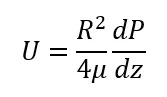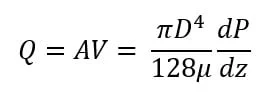If you try to solve for the velocity at any point in a three-dimensional, Newtonian fluid, the correct equations you must solve are the Navier-Stokes Equations.
Since we work in pipes, the form of that equations in cylindrical coordinates is shown below. Solving those equations doesn’t look like much fun.
They are nonlinear, partial differential equations which are about the worst kinds of equations to solve. About the only things that can make them worse are changes in state (e.g. steam condensing) or non-Newtonian fluids (e.g. mudflows). Numerous researchers have shown that it is impossible to arrive at a closed-form, analytical solution in the form v(r, φ, z) =… When people work with these equations these days, they almost always use numerical solutions.
I heard a story once that Albert Einstein started his research in solving the Navier-Stokes equations but gave up because it was too difficult. He moved on to easy topics like quantum physics and relativity. I haven’t been able to verify this, but it makes for a good story.
Since we’re interested in solving real-world engineering problems, why should we care about Navier-Stokes? We can trace many of our engineering solutions back to simplifications of these equations. First, for pipe flow, we don’t care much about the r and φ components. We can focus on the z components.
The left side of the equation is the mass (m) per unit volume times the accelerations (a) in the fluid, while the right side is the sum of the pressure, viscous, and gravity forces (F). So, all the Navier-Stokes equations are in a differential form of F = ma. You may have come across that equation somewhere.
Can we come up with an analytical solution to the z-equation for some special cases? Yes. First, let’s assume steady, uniform flow. This drops out all the acceleration terms on the left side and sets the left side to zero. That also drops out the φ term from the overall viscous stress term. We can combine the pressure and gravity forces into an overall pressure (i.e. head) gradient, which we’ll represent with a capital P. The viscous stress term is a nightmare in turbulent flow, so let’s assume we’re working in laminar flow. By using uniform flow, there are no changes in pipe diameters or inflows/outflow along the pipe, and dP/dz is a constant. (Yes, I realize that’s a lot of assumptions, but that’s what it takes to come up with something most engineers can solve with one semester of differential equations.) This results in
Where P = pressure/gravity force, μ = absolute viscosity u = z component of velocity and r, z are directions.
Integrating one time gives us
We need a boundary condition to get rid of the constant of integration, C1. We can use the fact that in laminar flow, the peak velocity occurs at the centerline of flow such that du/dr = 0 when r =0, which means that C1 = 0.
We can integrate again and get
The next boundary condition we need is the fact that the water doesn’t slip along the wall, such that u = 0 when r = R. This gives
Which means that the velocity profile in laminar flow is a parabola (i.e. u is a function of r squared).
We are usually interested in knowing the relationship between the average velocity and head loss. We need to integrate over the radius according to
Where U = average velocity and A = cross-sectional area.
This gives
Usually, we write this equation in terms of flow and diameter rather than velocity and radius and voila, we have the Hagen-Poiseuille equation (which makes up the laminar flow portion of the Moody diagram).
That wasn’t so difficult, was it? Now you can tell people that you can solve the Navier-Stokes equations (for a limited case).
Want to learn more from our resident water and wastewater expert? Join the Dr. Tom Walski Newsletter today!