We’re all familiar with the application of laws of conservation of mass and energy in models of water distribution systems. But did you know that there is also the Law of Conservation of Turbidity? 

Not really. Turbidity refers to the light scattering property of water. If light can’t penetrate a column of water, it has high turbidity. How can light scattering be conserved?

What is it that makes light have trouble penetrating into a column of water? It's suspended solids and solids have mass. We can write an equation for the mixing of two streams, each with its own solids concentration, to give the solids concentration in the mixture as:

Law of Conservation of Mass (suspended solids)

Q₁ C₁ + Q₂ C₂ = Q_o C_o                                                  (1)

Where Q is flow, C is concentration and the subscripts 1 and 2 are the two inflows and o refers to the outflow.

It’s easy to solve for the outflow concentration as

                                        (2)

If turbidity is caused by solids shouldn’t we be able to substitute turbidity in for solids and come up with

                                        (3)

If you take streams with equal flow, one with a turbidity of 10 and the other with 20, equation (3) says the resulting turbidity is 15. Is this true always, never, sometimes?

We did some lab research a few years back and showed that in some cases, the equation (3) could be used as a Law of Conservation of Turbidity. The key to applying that “Law” depends on the nature of the relationship between turbidity and solids concentration. We can write it as

C = f(T)                                                                     (4)

Substituting equation (4) into equation (2) which we know is true, gives us

                   (5)

Which can be considered to be the generalized Law of Conservation of Turbidity. If equation (4) is linear (i.e. C = aT), equation (5) can be written as

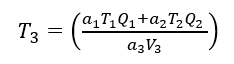                            (6)

If two streams have the same kind of solids, equation (6) collapses down to equation (3) as the a’s cancel out.

So, we ran a test on a variety of solids suspended in water, such as bentonite, kaolinite, iron oxide, and wetland soil.

We were able to show that two streams of the same material type could be mixed, and the result agreed with equation (3).

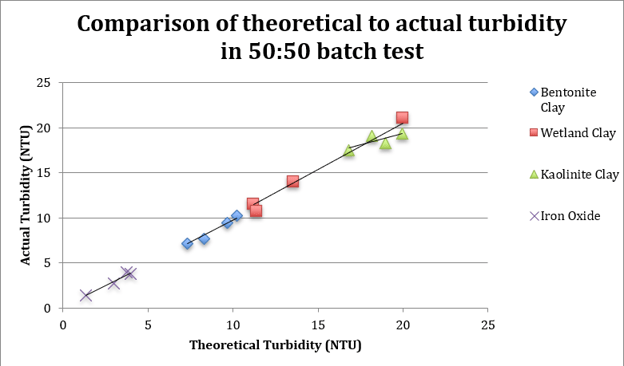
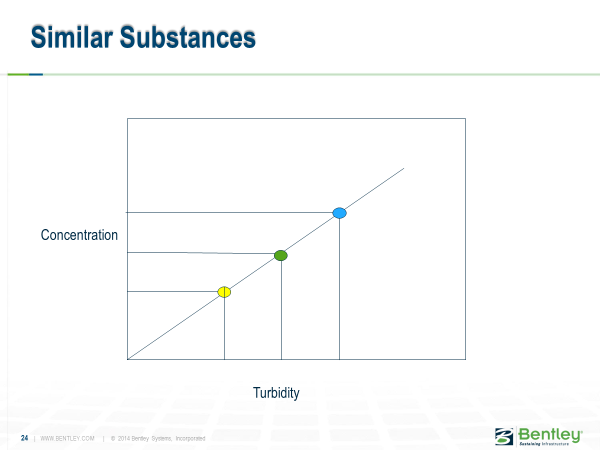
But when you mixed different kinds of solids, the a values did not cancel out, and you are left with a mystery of how to determine a₃ in equation (6). This problem is shown graphically in the figure below.

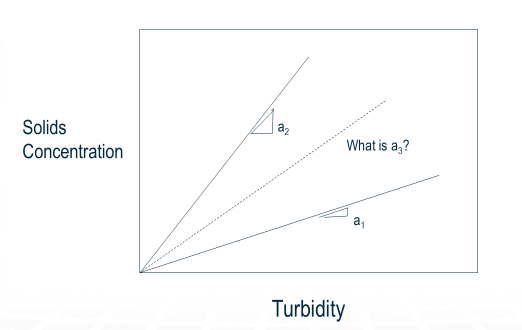
This can be explained graphically by considering that when you mix streams with blue concentration and yellow concentration, you get the concentration associated with the green point.

However, when you have different substances, you have different lines relating turbidity, and concentration, and the resulting turbidity could be any of the resulting red points.

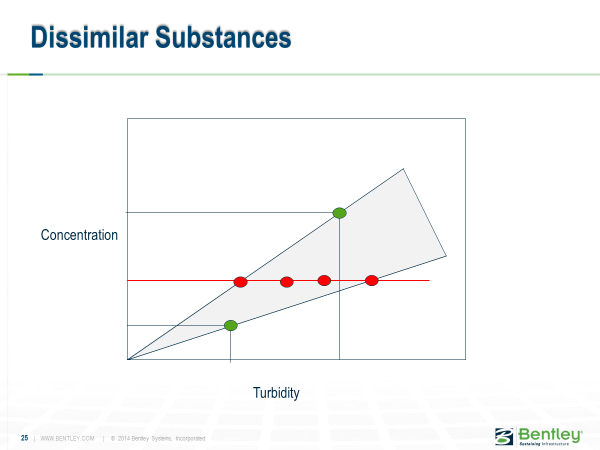
The conclusion from this work was that as long as you were mixing two streams where the nature of the solids was the same, and the relationship between solids concentration and turbidity was linear, equation (3) holds. However, if you tried to apply this to mixtures of different solids, you needed to use equation (5), and determining those functions could be difficult for the ensuing mixture.

Of course, there is the assumption that there is no chemical reaction between the solids, and they don’t precipitate or dissolve, but that’s also the case for equation (1) that everyone uses.

But we didn’t stop there. We didn’t want to just test this in lab beakers but in a water distribution system. We couldn’t introduce turbidity to a real system, so we build a small physical model in a hydraulics lab at Wilkes University. (The pipes are on the floor.)

And we built a hydraulic model of this system with WaterGEMS. Here are a few configurations.

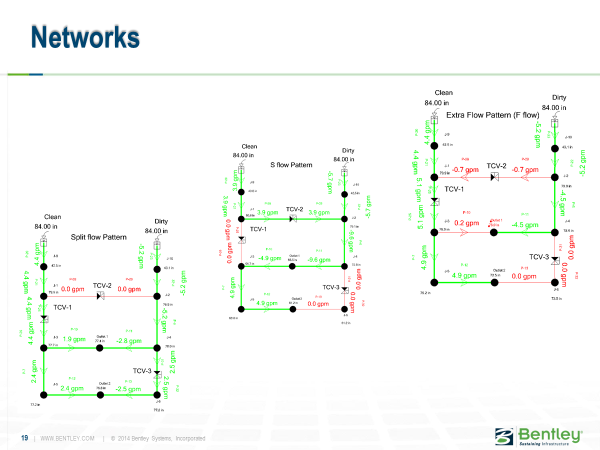
With the right valving, we could make all sorts of paths through the system, which had two inlets with different turbidity and two different outlet locations.

Once again, we ran a wide range of experiments at different solids, turbidities, flow rates, and flow paths. Here is an example of a case where the flow paths to the two outlets were significantly different. When they were similar, all the lines tended to converge as the model predicted.

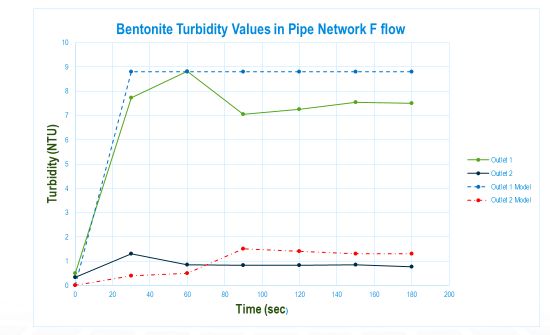
In summary, yes, there is a Law of Conservation of Turbidity, equation (5), provided you can come up with the C= f(T) function. More importantly, to the extent you are dealing with the same substance in all streams, it’s possible to use a simplified form, equation (3). The beauty of equation (3) is that it can readily be used in a water quality model like WaterGEMS, as that same equation is used in pretty much every water quality model of a water distribution system.

Reference

Walski, T., Minnich, K., Sharman, C., Stause, L. and Whitman, B., 2015, “Can There be a Law of Conservation of Turbidity,” Water Distribution System Analysis Conference, Cartagena, Colombia.

If you like blogs like this, you can go back to our library of blogs at https://blog.virtuosity.com/tag/water-and-wastewater. 

Want to learn more from our resident water and wastewater expert? Join the Dr. Tom Walski Newsletter today!