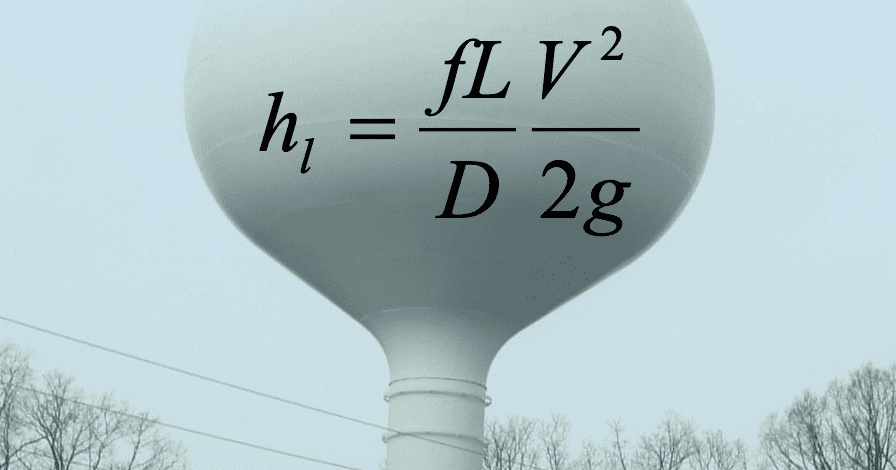An important step in selecting pumps is developing the system head curve, which gives the head needed to move various flow rates through a pumped system.
The shape of this curve depends on
- The lift to be provided between tank water levels on the suction and discharge sides of the pump
- Friction losses through the system.
If most of the energy goes to lifting the water, the curves are relatively flat since lift is independent of flow, while if most of the energy is used to overcome friction, the slope will be steep.
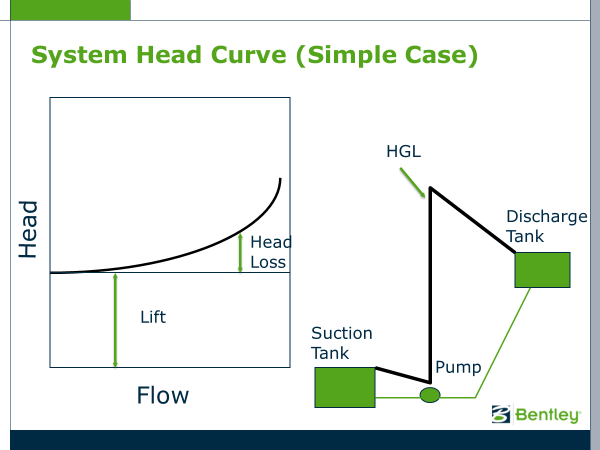
Simple Case
In the case where the flow moves from one tank to the next with a single pipe, the system head curve is easy to develop and can be done manually, as shown in Fig. 1 below.
Fig. 1
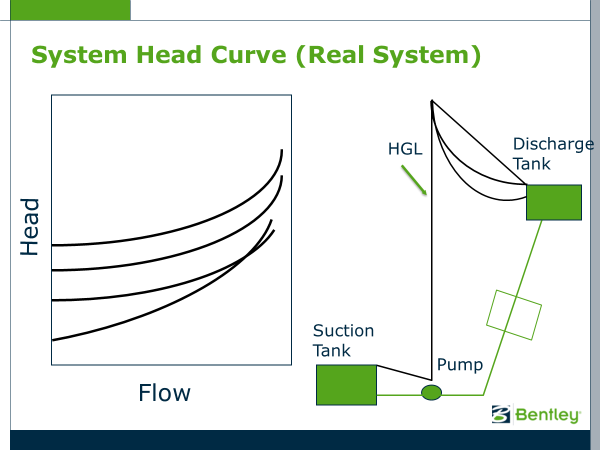
Real System
Real water and wastewater pumping system are more complicated to the extent that it is necessary to use a model such as WaterGEMS to develop these curves. Plus, there will be different curves for different combinations of tank levels and local demands.
Fig. 2
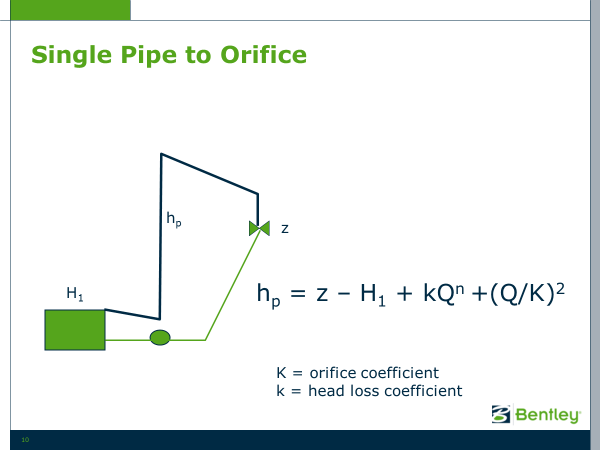
Dead end system
The problem becomes more difficult when pumping into a closed (dead end) system with no tank. In this case, determining the lift becomes problematic because there is no water surface to lift the water to. The water only reaches atmospheric pressure when it leaves an orifice (e.g. faucet, shower head, washing machine). Head loss through the orifices becomes important.
Fig. 3
If the water system only has a single orifice, it is easy to develop the curve with the equation in Fig. 3, but real water system feed thousands or millions or orifices, each at its own elevation. While water distribution system models, do not model every orifice, they do distribute demands to many nodes, each with its own demand and elevation. Using the fact that demands through orifices are pressure dependent, WaterGEMS can generate system head curves for systems with and without tanks with equal ease.
With and without tanks
How do system head curves for systems with and without tanks differ?
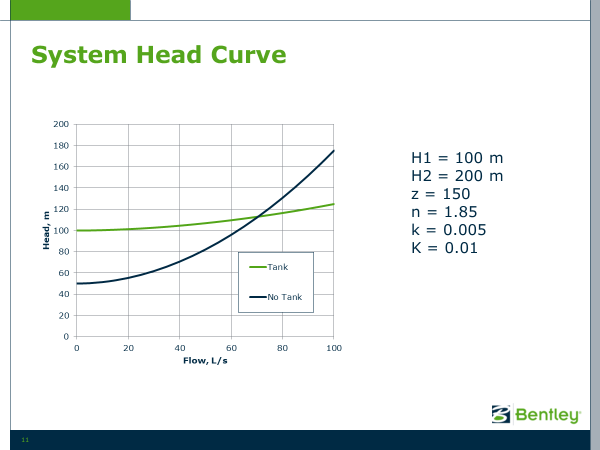
As shown in the Fig. 4 below, the hydraulic grade downstream of the pump doesn’t differ much as flow changes in systems with tanks. But with orifices flow, the hydraulic grade needed varies widely with demand and results in much steeper system head curves. This is shown below for a simple case.
Fig. 4
Temporal aspect of system head curves
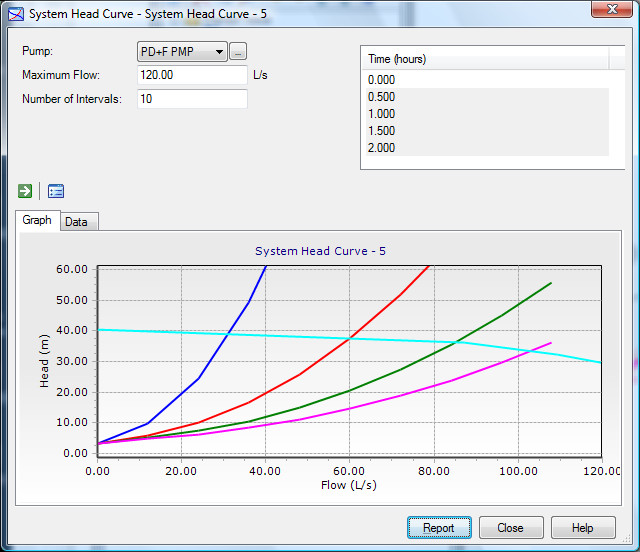
Then there is the temporal aspect of system head curves. In almost all cases, there is not a single system head curve but a band of curves that vary depending water levels in tanks, which other pumps are running, and demand patterns of users between the pump and the tanks/orifices. For systems with tanks, these variations are usually small, which results in a narrow band of curves. However, for systems with no tanks, the curves are very sensitive to demands and will vary widely from the peak hour of the day to time of minimum demands. The impacts of these variations on system head curves are shown in Fig. 5 below, taken from WaterGEMS.
Fig. 5
Some may argue that in closed systems, demands are not pressure dependent and the system head curve can be approximated by vertical lines corresponding to each demand. As can be seen in Fig. 5 above, the system head curves do not appear vertical.
The methods available in WaterGEMS make it easy to generate system head curves for systems that engineers couldn’t handle in the past.
Reference:
Walski, T., Hartell, W. and Wu, Z., 2010, “Developing System Head Curves for Closed Systems,” Journal AWWA, Vol. 102, No. 9. P. 84-89.
If you want to look up past blogs, go to https://blog.bentley.com/category/hydraulics-and-hydrology/.
If you want to contact me (Tom), you can email tom.walski@bentley.com.
Want to learn more from our resident water and wastewater expert? Join the Dr. Tom Walski Newsletter today!